Model

Model initialization and architecture.

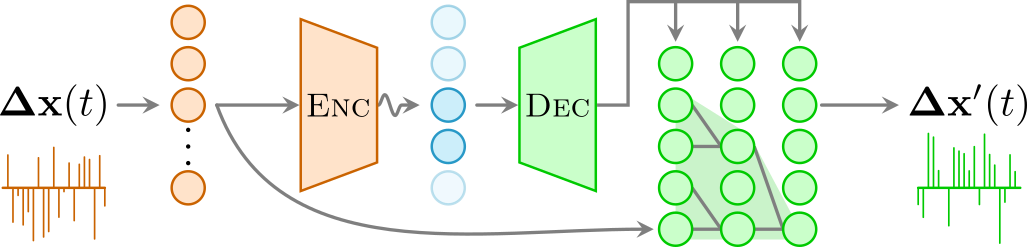
The architecture of the interpretable autoregressive \(\beta\)-VAE works in the following manner: Given the displacements \(\mathbf{\Delta x}(t)\) of a diffusion trajectory, the encoder (orange) compresses them into an interpretable latent space (blue), in which few neurons (dark blue) represent physical features of the input data while others are noised out (light blue). An autoregressive decoder (green) generates from this latent representation the displacements \(\mathbf{\Delta x}'(t)\) of a new trajectory recursively, considering a certain receptive field RF (light green cone).

Architecture

The models module provides:

• An autoregressive encoder-decoder architecture VAEWaveNet, implemented as an extension to a convolutional VAE VAEConv1d
• Initialization utilities for setting up convolutional layers
• Helper functions for computing output dimensions after convolution operations

After that, we show an example of how to instantiate and train one model.

Initialization

As the architecture can be quite deep, a careful initialization is needed (see weight_init function in the model class). We initialize the weights with normal Kaiming init in fan_out mode, taking into account that we use the nonlinear activation function ReLU.

---

source

init_cnn

def init_cnn(
    m:Module, # Module to initialize
):

Initialize module weights with kaiming normal in fan_out mode and bias to 0

VAE

We implement a 1D convolutional variational autoencoder as a base model.

Latent neurons

The latent neurons are probabilistic, i.e., they are sampled following a distribution. The reparameterization trick provides the means to allow backpropagation through these probabilistic neurons by externalizing the sampling noise.

---

source

reparameterize

def reparameterize(
    mu:Tensor, # Mean of the normal distribution, shape (batch_size, latent_dim)
    logvar:Tensor, # Diagonal log variance of the normal distribution, shape (batch_size, latent_dim)
)->Tensor: # Sampled latent z, shape (batch_size, latent_dim)

Sample latent tensor using the reparameterization trick: \(z=\epsilon\sigma+\mu\), where \(\epsilon\sim\mathcal{N}(0,1)\).

flowchart LR
    subgraph Inputs
        A["μ"]
        B["log σ²"]
    end
    
    B --> C["σ = exp(log σ² / 2)"]
    D(("ε ~ N(0,1)")) --> E["z = μ + σ·ε"]
    C --> E
    A --> E
    
    style A fill:#e1f5ff
    style B fill:#e1f5ff
    style D fill:#fff4e1
    style E fill:#e8f5e9

Output size helpers

We also take into account the sizes after n convolutions are applied to automate the model construction.

---

source

output_size_after_n_convt

def output_size_after_n_convt(
    n:int, input_size:int, kernel_size:int, stride:int=1, padding:int=0, output_padding:int=0, dilation:int=1
)->int:

---

source

output_size_convt

def output_size_convt(
    input_size:int, kernel_size:int, stride:int=1, padding:int=0, output_padding:int=0, dilation:int=1
)->int:

---

source

output_size_after_n_conv

def output_size_after_n_conv(
    n:int, input_size:int, kernel_size:int, stride:int=1, padding:int=0, dilation:int=1
)->int:

---

source

output_size_conv

def output_size_conv(
    input_size:int, kernel_size:int, stride:int=1, padding:int=0, dilation:int=1
)->int:

---

source

View

def View(
    size:tuple
):

Use as (un)flattening layer

1D Convolutional VAE

---

source

VAEConv1d

def VAEConv1d(
    nf:list, # number of filters
    encoder:list, # Encoder's dense layers sizes
    decoder:list, # Decoder's dense layers sizes
    o_dim:int, # input size (T)
    nc_in:int=1, # number of input channels
    nc_out:int=6, # number of output channels
    z_dim:int=6, # number of latent neurons
    beta:float=0.0, # weight of the KLD loss
    avg_size:int=24, # output size of the pooling layers
    kwargs:VAR_KEYWORD
):

1-dimensional convolutional VAE architecture

VAEConv1d Architecture Flow

flowchart LR
    A[Input] --> B[Conv1d]
    subgraph VAEConv1d
    subgraph Encoder
    B --> C[Adaptive<br>Pool<br>& Flatten]
    C --> D[Linear]
    D --> mu["μ"]
    D --> sigma["log σ²"]
    end
    epsilon(("ε ~ N(0,1)")) --> F
    subgraph Latent
    mu --> F["Reparameterize<br>z = μ + σ·ε"]
    sigma --> F
    end
    subgraph Decoder
    F --> G[Linear]
    G --> H[Unflatten &<br>Interpolate]
    H --> I[Conv1d<br>Transpose]
    end
    end
    I --> J[Output]
    
    style A fill:#e1f5ff
    style F fill:#fff4e1
    style J fill:#e8f5e9

VAE + WaveNet

We extend the VAE with WaveNet as the autoregressive decoder.

---

source

sample_from_mix_gaussian

def sample_from_mix_gaussian(
    y:Tensor, # Mixture of Gaussians parameters. Shape (B x C x T)
    log_scale_min:float=-12.0, # Log scale minimum value.
)->Tensor:

Sample from (discretized) mixture of gaussian distributions.

---

source

DilatedCausalConv1d

def DilatedCausalConv1d(
    mask_type:str, in_channels:int, out_channels:int, kernel_size:int=2, dilation:int=1, bias:bool=True,
    use_pad:bool=True
):

Dilated causal convolution for WaveNet

---

source

ResidualBlock

def ResidualBlock(
    res_channels:int, skip_channels:int, kernel_size:int, dilation:int, c_channels:int=0, g_channels:int=0,
    bias:bool=True, use_pad:bool=True
):

Residual block with conditions and gate mechanism

ResidualBlock Architecture Flow

flowchart LR
    C[Local<br>Conditioning<br>c] --> D[Conv1d 1x1]-->C2[Chunk]-->c1-->sum1
    C2-->c2-->sum2
    A[Input<br>x] --> B[Dilated<br>Causal<br>Conv1d]-->Chunk-->o1-->sum1[+]
    Chunk-->o2-->sum2[+]
    sum2 --> H
    sum1 --> G
    subgraph Gated Activation
        H[sigmoid]-->*
        G["id #tanh"]-->*
    end
    * --> K[Conv1d 1x1] --> N[Skip<br>Output]
    * --> J[Conv1d 1x1] --> L[+] --> M[Residual<br>Output]
    A --> L
    
    style A fill:#e1f5ff
    style C fill:#e1f5ff
    style M fill:#e8f5e9
    style N fill:#fff4e1

---

source

VAEWaveNet

def VAEWaveNet(
    in_channels:int=1, # input channels
    res_channels:int=16, # residual block channels
    skip_channels:int=16, # skip connection channels
    c_channels:int=6, # local conditioning (time-wise)
    g_channels:int=0, # global conditioning (the same for the whole sequence)
    out_channels:int=1, # output channels
    res_kernel_size:int=3, # kernel_size of dilated layers in residual blocks
    layer_size:int=4, # largest dilation is 2^layer_size
    stack_size:int=1, # number of layers stacks
    out_distribution:str='normal', discrete_channels:int=256, num_mixtures:int=1, # 1=no mixture
    use_pad:bool=False, weight_norm:bool=False, kwargs:VAR_KEYWORD
):

VAE with autoregressive decoder

VAEWaveNet Architecture Flow

flowchart LR
    A[Input<br>x] --> B[VAEConv1d] --> C[Local<br>Conditioning<br>c]-->W[WaveNet]
    A-->W[WaveNet]-->O[Output<br>Probability]

WaveNet Architecture Flow

flowchart LR
    C[Local<br>Conditioning<br>c] --> R
    C-.->R2
    C-->R3
    A[Input<br>x] --> B[Conv1d 1x1]--> D[Dilated<br>Causal<br>Conv1d]--> R[Residual<br>Block]
    subgraph RS["Residual Stack"]
    R -.-> R2["···"] -.-> R3[Residual<br>Block]
    end
    R  --> s1
    R2 -.-> s2
    R3 --> s3
    %% the plus sign alone is interpreted as markdown list, thus #43;
    S["Skip=0"] -->s1(("#43;"))-.->s2(("#43;"))-.->s3(("#43;"))-->Conv1d-->O[Output]

We can create a model by specifying its parameters in a dict.

model_args = dict(# VAE #########################
                  o_dim=400,
                  nc_in=1, nc_out=6,
                  nf=[16]*4,
                  avg_size=16,
                  encoder=[200,100],
                  z_dim=6,
                  decoder=[100,200],
                  beta=0,
                  # WaveNet ########
                  in_channels=1,
                  res_channels=16,skip_channels=16,
                  c_channels=6,
                  g_channels=0,
                  res_kernel_size=3,
                  layer_size=4,  # 6
                  stack_size=1,
                  out_distribution= "Normal",
                  num_mixtures=1,
                  use_pad=False,
                  model_name = 'SPIVAE',
                 )
model = VAEWaveNet(**model_args)

Printing the model object will reveal the declared layers.

model

VAEWaveNet(
  (vae): VAEConv1d(
    (encoder): Sequential(
      (0): Conv1d(1, 16, kernel_size=(3,), stride=(1,))
      (1): ReLU(inplace=True)
      (2): Conv1d(16, 16, kernel_size=(3,), stride=(1,))
      (3): ReLU(inplace=True)
      (4): Conv1d(16, 16, kernel_size=(3,), stride=(1,))
      (5): ReLU(inplace=True)
      (6): Conv1d(16, 16, kernel_size=(3,), stride=(1,))
      (7): ReLU(inplace=True)
      (8): AdaptiveConcatPool1d(
        (ap): AdaptiveAvgPool1d(output_size=16)
        (mp): AdaptiveMaxPool1d(output_size=16)
      )
      (9): View()
      (10): Linear(in_features=512, out_features=200, bias=True)
      (11): ReLU(inplace=True)
      (12): Linear(in_features=200, out_features=100, bias=True)
      (13): ReLU(inplace=True)
      (14): Linear(in_features=100, out_features=12, bias=True)
    )
    (decoder): Sequential(
      (0): Linear(in_features=6, out_features=100, bias=True)
      (1): ReLU(inplace=True)
      (2): Linear(in_features=100, out_features=200, bias=True)
      (3): ReLU(inplace=True)
      (4): Linear(in_features=200, out_features=512, bias=True)
      (5): ReLU(inplace=True)
      (6): View()
    )
    (convt): Sequential(
      (0): ConvTranspose1d(16, 16, kernel_size=(3,), stride=(1,))
      (1): ReLU(inplace=True)
      (2): ConvTranspose1d(16, 16, kernel_size=(3,), stride=(1,))
      (3): ReLU(inplace=True)
      (4): ConvTranspose1d(16, 16, kernel_size=(3,), stride=(1,))
      (5): ReLU(inplace=True)
      (6): ConvTranspose1d(16, 6, kernel_size=(3,), stride=(1,))
      (7): ReLU(inplace=True)
    )
  )
  (init_conv): Conv1d(1, 16, kernel_size=(1,), stride=(1,))
  (causal): DilatedCausalConv1d(
    (conv): Conv1d(16, 16, kernel_size=(2,), stride=(1,))
  )
  (res_stack): ModuleList(
    (0): ResidualBlock(
      (dilated): DilatedCausalConv1d(
        (conv): Conv1d(16, 32, kernel_size=(3,), stride=(1,))
      )
      (conv_c): Conv1d(6, 32, kernel_size=(1,), stride=(1,), bias=False)
      (conv_res): Conv1d(16, 16, kernel_size=(1,), stride=(1,))
      (conv_skip): Conv1d(16, 16, kernel_size=(1,), stride=(1,))
    )
    (1): ResidualBlock(
      (dilated): DilatedCausalConv1d(
        (conv): Conv1d(16, 32, kernel_size=(3,), stride=(1,), dilation=(2,))
      )
      (conv_c): Conv1d(6, 32, kernel_size=(1,), stride=(1,), bias=False)
      (conv_res): Conv1d(16, 16, kernel_size=(1,), stride=(1,))
      (conv_skip): Conv1d(16, 16, kernel_size=(1,), stride=(1,))
    )
    (2): ResidualBlock(
      (dilated): DilatedCausalConv1d(
        (conv): Conv1d(16, 32, kernel_size=(3,), stride=(1,), dilation=(4,))
      )
      (conv_c): Conv1d(6, 32, kernel_size=(1,), stride=(1,), bias=False)
      (conv_res): Conv1d(16, 16, kernel_size=(1,), stride=(1,))
      (conv_skip): Conv1d(16, 16, kernel_size=(1,), stride=(1,))
    )
    (3): ResidualBlock(
      (dilated): DilatedCausalConv1d(
        (conv): Conv1d(16, 32, kernel_size=(3,), stride=(1,), dilation=(8,))
      )
      (conv_c): Conv1d(6, 32, kernel_size=(1,), stride=(1,), bias=False)
      (conv_res): Conv1d(16, 16, kernel_size=(1,), stride=(1,))
      (conv_skip): Conv1d(16, 16, kernel_size=(1,), stride=(1,))
    )
  )
  (out_conv): Sequential(
    (0): ReLU(inplace=True)
    (1): Conv1d(16, 16, kernel_size=(1,), stride=(1,))
    (2): ReLU(inplace=True)
    (3): Conv1d(16, 9, kernel_size=(1,), stride=(1,))
  )
)

Training a VAEWaveNet

The following example demonstrates a complete training workflow: loading data, initializing the model, and training with fastai’s Learner.

DEVICE= 'cpu' # 'cuda'
print(DEVICE)

cpu

N=6_000

Ds = np.linspace(2e-5,2e-2,5)
alphas = np.linspace(0.2,1.8,9)
n_alphas,n_Ds = len(alphas), len(Ds)
ds_args = dict(path="../../data/raw/", model='fbm', # 'sbm'
               N=int(N/n_alphas/n_Ds*2), T=400,
               D=Ds, alpha=alphas,seed=0,
               valid_pct=0.2, bs=2**8,
               N_save=N, T_save=400,
              )

model_args = dict(# VAE ###########################
                  o_dim=ds_args['T']-1,
                  nc_in=1, nc_out=6,
                  nf=[16]*4,
                  avg_size=16,
                  encoder=[200,100],
                  z_dim=6,
                  decoder=[100,200],
                  beta=0,
                  # WaveNet ########
                  in_channels=1,
                  res_channels=16,skip_channels=16,
                  c_channels=6,
                  g_channels=0,
                  res_kernel_size=3,
                  layer_size=4,  # 6  # Largest dilation is 2**layer_size
                  stack_size=1,
                  out_distribution= "Normal",
                  num_mixtures=1,
                  use_pad=False,
                  model_name = 'SPIVAE',
                 )

dls = load_data(ds_args)

model = VAEWaveNet(**model_args).to(DEVICE)

loss_fn = Loss(model.receptive_field, model.c_channels,
               beta=model_args['beta'], reduction='mean')

learn = Learner(dls, model, loss_func=loss_fn,)

E=4

learn.fit_one_cycle(E, lr_max=1e-4)

epoch	train_loss	valid_loss	time
0	0.982180	0.949590	00:28
1	0.934559	0.880010	00:25
2	0.882010	0.822553	00:26
3	0.843744	0.810182	00:29